Welcome to the eight installment of Predictions of the 10th Justice, brought to you by FantasySCOTUS.net. The league has over 3,600 members, who have made predictions on all cases currently pending before the Supreme Court.
How many SCOTUS watchers does it take to accurately predict the outcome of a case? How large of a crowd do we need before the crowd becomes “wise”? The wisdom of the crowds considers the accuracy of the collective opinion of a group, which in many cases may be more reliable than the opinion of experts. In this column, the 10th Justice tests the theory of the wisdom of the crowds. Based on the accuracy of our predictions in Citizens United v. FEC, the landmark campaign finance reform case, we will develop levels of confidence to determine how reliable our predictions are for four of the most significant cases this term.
There are two major components of interval calculation: sample size and confidence level. Sample size refers to the number of members who predict a certain cases. A confidence interval indicates the certainty that the margin of error is correct. Confidence intervals, commonly known as margins of error, indicate the proportion of members, out of all members, who predicted a specific outcome of a case. One can never be 100% sure that a margin of error is correct. For example, if 56% of our members predicts that the Supreme Court will reverse the lower court, and the margin of error is 3%, the actual proportion of members who vote to reverse will be somewhere between 53% and 59%.
If one is 90% sure that a margin of error is correct, that indicates there is a 10% chance that the margin of error wrong. Similarly, if one is 95% sure that a margin of error is correct, that indicates there is a 5% chance that the margin of error is wrong. Finally, if one is 99% sure that a margin of error is correct, that indicates there is a 1% chance that the margin of error is wrong. In order to establish a higher confidence level, one must increase the margin of error. While this makes the results more reliable, as the confidence level is higher, the increased range yields less accuracy. Analyzing the sample size and confidence level allows the 10th Justice to make predictions, with varying degrees of certainty, about the outcomes of cases.
To determine confidence intervals, we analyzed the results from Citizens United. We considered sample sizes of 908, 286 (our results in mid-November), and random samples of 100, 50, and 25 members.
Given a sample size of 908 members, we are 90% certain that the true value lies within 2.65 percentage points of 62%. When we say 62% will vote for reversal, we are 90% certain that the actual prediction value for reversal lies between 59.35% and 64.65%. When we say 62% will vote for reversal, we are 95% certain that the actual prediction value for reversal lies between 62-3.16 and 62+3.16. When we say 62% will vote for reversal, we are 99% certain that the actual prediction value for reversal lies between 62-4.15% and 62.415%.
Once the range drops below 50%, we cannot definitively state that our members are more for or against reversal. Given a sample size of 50 predictions, when we say 62% will vote for reversal, we are 90% certain that the actual prediction value for reversal lies between 48.55% and 75.45%. The lower boundary drops below 50%, and thus below our critical value, and we can no longer reliably say with any certainty which way our members will vote. The columns highlighted in red indicate values that drop below the critical level.
Based on these confidence intervals, we can state, with accuracy how reliable are predictions are for four major cases this term. We test:
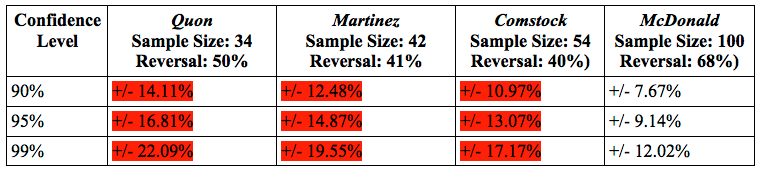
- City of Ontario v. Quon, which considers whether a public employees have a right to privacy for text messages on their electronic pagers
- Christian Legal Society v. Martinez, which considers funding for religious student organizations that require members to share their religious views
- McDonald v. Chicago, which considers whether the 2nd amendment should be incorporated to the states
- United States v. Comstock, which considers the constitutionality of continued imprisonment of a sex offender, after that individual has completed serving a prison sentence for the crime.
In Quon, considering a sample size of 34 predictions, 50% of the votes predicted a reversal. In Martinez, considering a sample size of 42 predictions, 41% of the votes predicted a reversal. In Comstock, considering a sample size of 54 predictions, 40% of the votes predicted a reversal. Finally, in McDonald, considering a sample size of 100 predictions, 68% predicted a reversal. In Quon, Martinez, and Comstock, because the margins of error are so large, we cannot predict with at least a 90% level of confidence that this prediction is accurate. In McDonald, we can predict with up to 99% confidence that the Supreme Court will reverse the lower court.
Based on this data, we assume that a case needs more than 50 votes in order to produce a confident estimate of the outcome, except when the vote is split 50%. Going forward, any case with less than 50 votes will likely not yield reliable results.
Thanks to Corey Carpetner for his stellar help with this post.